如图，在△ABC中，AB>AC，∠1=∠2，P为AD上任意一点．求证：AB-AC>PB-PC．
答案
证明：如图，在线段AB上截取AE=AC，连接PE．
则AB-AC=AB-AE=EB
在△AEP和△ACP中
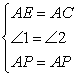
∴△AEP≌△ACP（SAS）
∴PE=PC在△PEB中，PB-PE<EB
∴PB-PC<AB-AC
即AB-AC>PB-PC
（延长AC到点F，使AF=AB，连接PF，也可证明结论）
知识点：三角形全等之截长补短
略
略
WORD格式（
