已知:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.
(1)求证:EF=EG.

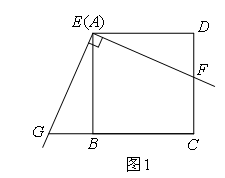
解题思路:(1)由正方形ABCD可以得到条件∠D=∠EBG=∠BED=90°,ED=EB;又因为∠FEG=90°,根据           ,得到∠BEG=∠DEF;利用全等三角形的判定定理           ,证明           ,根据全等的性质可以得到EF=EG.
①同角的补角相等,②同角的余角相等,③△EDF≌△EBG,④△EDF≌△EGB,⑤AAS,⑥ASA
以上横线处,依次所填正确的是(    )

• A.①⑥③
• B.②⑥④
• C.②⑥③
• D.②⑤③
  

答案

正确答案：C

知识点：三角形全等之类比探究  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>