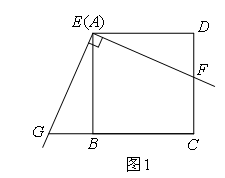
已知:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其它条件不变,(1)中的结论(EF=EG)是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
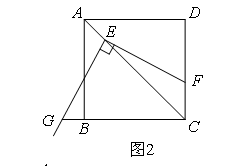
解题思路:(2)类比第(1)问的思想,构造两个直角三角形,证明全等;添加辅助线为 ;所以∠EMC=∠ENC=90°,在正方形ABCD中,∠ACB=∠ACD=45°,∠MEC=∠NEC=45°,又因为CE是公共边,所以利用全等三角形的判定定理 ,证明 ,进而得到EM=EN,因为∠GEF=∠MEN=90°,根据同角的余角相等可以得到∠MEG=∠NEF,利用全等三角形的判定定理 ,证明 .
①过点E作EM⊥BC于M,过点E作EN⊥DC于N;②过点E作EM⊥AB于M,过点E作EN⊥AD于N;③ASA;④AAS;⑤△EMC≌△ENC;⑥△EMG≌△ENF;
以上横线处,依次所填正确的是( )
- A.①③⑤④⑥
- B.①④⑥③⑤
- C.②④⑤③⑥
- D.①④⑤③⑥
答案
正确答案:D
知识点:三角形全等之类比探究
略
略









