如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从点A出发，沿着AB向点B运动；同时点Q从点C出发，沿CA向点A运动，当点P到达点B时，点Q随之停止运动．已知．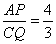
（1）当AP为何值时，PQ∥BC？
（2）△APQ与△CQB能否相似？若能，求出AP的长；若不能，说明理由．

答案

解：（1）由题意：设AP=4x，则CQ=3x，AQ=30-3x，
当PQ∥BC时，，即：
解得：
此时：AP=cm
∴当AP=cm时，PQ∥BC
（2）能，AP=cm或AP=20cm
①△APQ∽△CBQ，则，即
解得：或（舍）
此时：AP=cm
②△APQ∽△CQB，则，即
解得：（符合题意）
此时：AP=cm
故AP=cm或20cm时，△APQ与△CQB能相似．

知识点：相似中的存在性问题  

略

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>