如图，在Rt△ABC中，ACB=90°，AC=6，BC=8，点D在边AB上运动，DE平分CDB交边BC于点E，EM⊥BD，垂足为M，EN⊥CD，垂足为N．
（1）当AD=CD时，求证：DE∥AC．
（2）探究：是否存在这样的AD，使得△BME与△CNE相似？

答案

解：（1）证明：∵AD=CD
∴∠A=∠ACD
∵DE平分ACD交边BC于点E
∴∠CDE=∠BDE
∵∠CDB为△CDB的一个外角
∴∠CDB=∠A+∠ACD=2∠ACD
∵∠CDB=∠CDE+∠BDE=2∠CDE
∴∠ACD=∠CDE
∴DE∥AC
（2）存在
∵在Rt△ABC中，ACB=90°，AC=6，BC=8
∴AB=10
①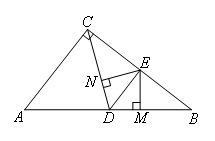
当∠NCE=∠MBE时
∵EM⊥BD，EN⊥CD，
∴△BME∽△CNE
∵∠MBE=∠NCE
∴BD=CD
∵∠NCE+∠ACD=∠MBE+∠A=90°
∴∠ACD=∠A
∴AD=CD
∴AD=BD=AB=5
②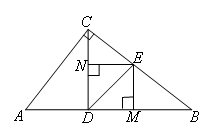
当∠NCE=∠MEB时
∵EM⊥BD，EN⊥CD，
∴△BME∽△ENC
∵∠NCE=∠MEB
∴EM∥CD
∴CD⊥AB
∵∠A=∠A，∠ADC=∠ACB
∴△ACD∽△ABC
∴
∴
综上：AD=5或时，△BME与△CNE相似．