如图1，在四边形ABCD中，∠D=90°，BC∥AD，BC=20，DC=16，AD=30．动点P从点D出发，沿射线DA方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动．设运动时间为t（秒）．
（1）设△BPQ的面积为S，求S与t之间的函数关系式．
（2）当t为何值时，使得线段PQ与线段AB相交于点O，且2AO=OB？
（3）当t为何值时，使得PQ⊥BD？
（4）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？

答案

解：（1）由题意得：CQ=t
∴BQ=20-t
∴S=(20-t)×16=-8t+160
（2）如果线段PQ与线段AB相交，则P点应运动到A点的左侧，此时15<t≤20
由题意得：AP=2t-30，△BOQ∽△AOP
∴=2
即
∴t=16
即：当t=16s时，2AO=OB
（3）

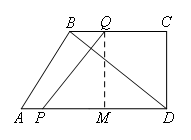
当PQ⊥BD时，过点Q作QM⊥AD交AD于点M
由题意得：PM=PD-MD=PD-CQ=t，△PQM∽△DBC
∴
即：
∴t=12.8s
（4）

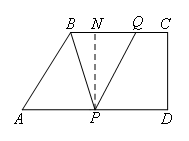
过点P作PN⊥BC于点N
①PB=PQ时，BN=NQ，即：20-2t=t，解得t=；
②当PQ=BQ时，t²+16²=(20-t)²，解得t=；
③当BQ=PB时，无解．
综上，当t=s或s时，以B，P，Q三点为顶点的三角形是等腰三角形．

知识点：相似之动点问题  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>