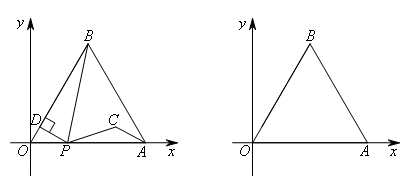
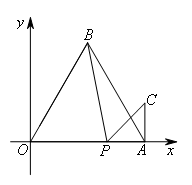
如图，边长为4的等边三角形AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限．一动点P从O点出发沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t（秒）．将线段BP的中点绕点P按顺时针方向旋转60°得到点C，点C随点P的运动而运动，连接CP，CA，过点P作PD⊥OB于点D。
（1）填空：PD的长为 （用含t的代数式表示）．
（2）求点C的坐标（用含t的代数式表示）．
（3）在点P从O向A运动的过程中，△PCA能否成为直角三角形？若能，求出t的值；若不能，请说明理由．
答案
解：（1）
（2）
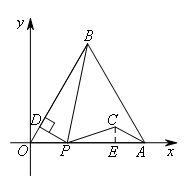
过C作CE⊥OA于E
∴∠PEC=90°
由题意知：OD=
t
∴BD=4-t
∵线段BP的中点绕点P按顺时针方向旋转60°得点C
∴∠BPC=60°
∵∠OPD=30°
∴∠BPD+∠CPE=90°
∵∠BPD+∠DBP=90°
∴∠DBP=∠CPE
∴△PCE∽△BPD
∴
即：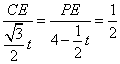
∴CE=
，PE=2-
t
∴OE=2+
t
∴C(2+t，)
（3）能
①
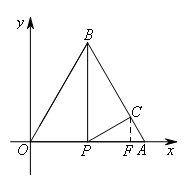
当∠PCA=90°时，作CF⊥PA
∴△PCF∽△CAF
∴
∴
∵PF=2-t，AF=4-OF=2-t，CF=
∴
∴t=2，此时P是OA的中点．
②
当∠CAP=90°时，C的横坐标就是4
∴2+t=4
∴t=
综上，当t=2s或s时，△PCA能成为直角三角形．
知识点：相似之动点问题
略
略
WORD格式（
