如图，已知一次函数y=-x+7与正比例函数y=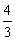
x的图象交于点A，且与x轴交于点B．过点A作AC⊥y轴于点C，过点B作直线l∥y轴．动点P从点O出发，以每秒1个单位长的速度，沿O→C→A的路线向点A运动，同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P的运动时间为t（秒）．
（1）求点A和点B的坐标．
（2）当t为何值时，以A，P，R为顶点的三角形的面积为8？
（3）是否存在以A，P，Q为顶点的三角形是等腰三角形？若存在，求出t的值；若不存在，请说明理由．
x的图象交于点A，且与x轴交于点B．过点A作AC⊥y轴于点C，过点B作直线l∥y轴．动点P从点O出发，以每秒1个单位长的速度，沿O→C→A的路线向点A运动，同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P的运动时间为t（秒）．
答案
解：（1）由题意得：A为y=-x+7与
交点
联立得
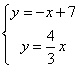，解得
∴A(3，4)
∵B为y=-x+7与x轴交点
∴B(7，0)
（2）
①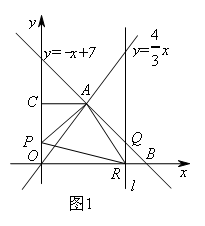
如图1所示，当0≤t≤4时，点P在线段OC上
则P(0，t)，R(7-t，0)
∵A（3，4），AC⊥y轴
∴AC=3，OC=4
∵OP=t
∴CP=4-t
∴S△ACP=
=
∵BR=t，OB=7
∴OR=7-t
∴S△OPR=
=
∴S△APR=S梯形ACOR-S△ACP-S△OPR
=
=
若S△APR=8，则=8，即t=2或t=6（舍）
②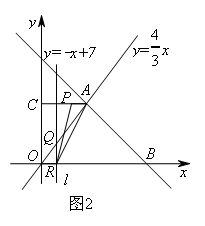
如图2所示，当4<t<7时，点P在线段AC上
∵OC+CP=t，OC+AC=7
∴AP=7-t
∴S△APR=
=-2t+14
若S△APR=8，则-2t+14=8，即t=3（舍）
综上，t=2时，S△APR=8.
（3）存在
①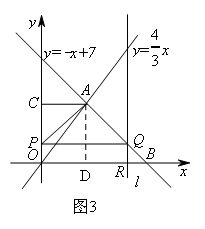
如图3所示，当0≤t≤4时，点P在线段OC上，过A作AD⊥x轴于点D，
则OD=AC=3，AD=OC=4
∴OA=5，BD=OB-OD=4
∴∠ABO=45°
∴AB=
∵l∥y轴
∴QR=BR=t
∵OP=t
∴PQ∥x轴
此时欲使△APQ为等腰三角形，显然只有使AP=AQ
在Rt△ACP中，AC=3，CP=4-t，
∴
在Rt△BRQ中，∠QBR=45°
∴QB=
，
=
=
若AP=AQ，则t=1或t=7（舍）
②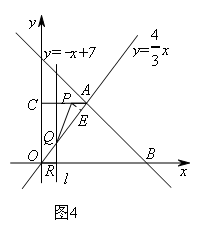
如图4所示，当4<t<7时，点P在线段AC上
则AP=7-t，OR=7-t
∵△OQR∽△AOC
∴
∴OQ=
∴AQ=
若AP=AQ则t=
若AP=PQ，过点P作PE⊥AQ于点E，则AE=
AQ=
∵∠PEA=90°，∠PAE=∠OAC
∴△PAE∽△OAC
∴
即：=
解得t=
若AQ=PQ
类比上一种情况，可以解得t=5
综上，当t的值为1s或s或s或5s，以A，P，Q为顶点的三角形是等腰三角形．
知识点：相似中的动点问题
略
略
WORD格式（
