如图，直角梯形OABC中，AB∥OC，其中O(0，0)，A(0，
)，B(4，)，C(8，0)，OH⊥BC于点H。
（1）求∠HOC的度数．
（2）动点P从点O出发，沿线段OH向点H运动，动点Q从点A出发，沿线段AO向点O运动，两点同时出发，速度均为每秒1个单位长度，设运动时间为t（秒）．
①若直线QP交x轴的正半轴于点N，当t为何值时，QP=2PN？
②在P，Q运动过程中，是否存在t值，使得△OPQ与△HOB相似，若存在，求出t的值；若不存在，请说明理由．
答案
解：（1）由题意得：OA=
，AB=4，∠OAB=90°，OC=8
∴OB=8，∠AOB=30°
∴∠BOC=60°，OC=OB
即：△BOC是等边三角形
∵OH⊥BC
∴∠HOC=30°
（2）①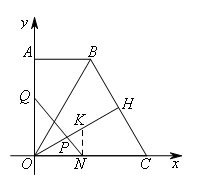
过点N作NK⊥x轴交OH于点K
∴△POQ∽△PKN
如果QP=2PN，则
由题意得：OQ=－t，OP=t
∴PK=
t，NK=(－t)
∴OK=
t
∵∠HOC＝30°
∴
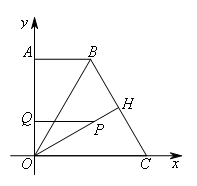
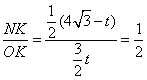
∴t＝
②存在
当QP⊥OH时，△OPQ∽△HOB
∵∠QOP=60°
∴
∴t=
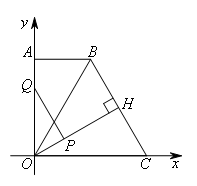
当PQ⊥OA时，△OPQ∽△BOH
则
∴t=
综上，当t=s或s时，△OPQ与△HOB相似．
知识点：相似之动点问题
略
略
WORD格式（
