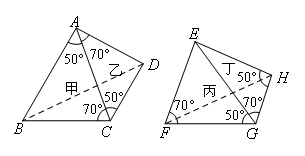
如图,两个三角锥ABCD、EFGH,其中甲、乙、丙、丁分别表示△ABC,△ACD,△EFG,△EGH.
若∠ACB=∠CAD=∠EFG=∠EGH=70°,∠BAC=∠ACD=∠EGF=∠EHG=50°,则下列叙述一定正确的是(    )

全等三角形的5种判定方法：AAS、SAS、ASA、SSS、HL，判断三角形是否全等，必须依据这5种方法.根据选项可知，需要判断的是甲和乙、丙和丁是否全等，观察图形得到，甲、乙中∠ACB=∠CAD，∠BAC=∠ACD，还隐藏的一个条件是AC=CA，根据ASA可以判断△ABC≌△CDA，所以甲、乙一定全等；而对于丙、丁，∠EFG=∠EGH，∠EGF=∠EHG，还有就是EG=EG是隐含的公共边，初看可以利用AAS来判定，但是仔细观察就会发现，EG所对的角一个是70°，一个是50°，所以两个图形不能完全重合，故不全等，选B．

略