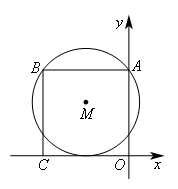
如图,在平面直角坐标系中,正方形ABCO的顶点A,C分别在y轴,x轴上,以AB为弦的⊙M与x轴相切.若点A的坐标为(0,8),则圆心M的坐标为(    )

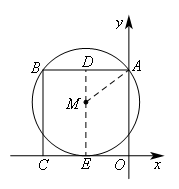如图，过点M作MD⊥AB于D，交OC于点E．连接
AM，设⊙M的半径为R．
∵以边AB为弦的⊙M与x轴相切，AB∥OC，
∴DE⊥CO，∴DE是⊙M直径的一部分；
∵四边形OABC为正方形，顶点A，C在坐标轴上，点A的坐标为（0，8），
∴OA=AB=CB=OC=8，DM=8-R；∴AD=BD=4（垂径定理）；
在Rt△ADM中，根据勾股定理可得，
∴，∴R=5．∴M（-4，5）．

略