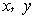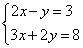若等腰三角形的两边长满足方程组,则此等腰三角形的周长为(    )

（1）考点：解二元一次方程组；等腰三角形的性质；三角形三边关系．
（2）解答过程：，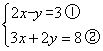
由①，得，
把③代入②，得x=2，
把x=2代入③，得y=1，
∴原方程组的解为．
所以，等腰三角形的两边长为2，1．
若腰长为1，底边长为2，由1+1=2知，这样的三角形不存在．
若腰长为2，底边长为1，则三角形的周长为5．
所以，这个等腰三角形的周长为5．故选D．
（3）易错点：没有考虑三角形的三边关系．

略