如图,在△ABC中,D是BC上一点,且满足AD=AC.E是AD的中点,且满足∠BAD=∠ACE.若S_△BDE=1,则S_△ABC为(    )

如图，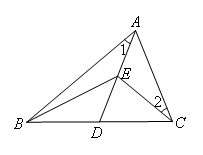

∵E是AD的中点，
∴，
∵∠CED=∠2+∠CAE，∠BAC=∠1+∠CAE，∠1=∠2
∴∠CED=BAC，
∵AD=AC，
∴∠CDE=∠BCA，
∴△CED∽△BAC，且DE：AC=1:2．
设△CED的面积为x，则△ABC的面积为4x，
∴，解得
∴S_△ABC=4．

略