已知两点M(3,5),N(1,1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为( )
- A.(
 ,0)
,0) - B.(
 ,0)
,0) - C.(
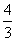 ,0)
,0) - D.(
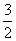 ,0)
,0)
答案
正确答案:C
知识点:一次函数综合题
(1)考点:两点之间线段最短,待定系数法求表达式,直线与x轴的交点坐标
(2)解答过程:
点N关于x轴的对称点N′的坐标为(1,-1)
若使PM+PN最短,即PM+PN′最短
∴M,P,N′三点共线,
∵M(3,5),N′(1,-1),
∴设经过M,N′两点的直线解析式为y=kx+b,
把M(3,5),N′(1,-1)分别代入解析式得:![]()
解得:![]()
即解析式为y=3x-4
当y=0时,x=![]()
故P点坐标为(![]() ,0)
,0)
故选C.
略







