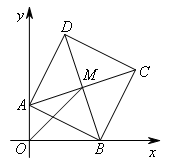
如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标是(0,2),顶点B在x轴上,
对角线AC,BD交于点M,OM=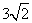 ,则点C的坐标是( )
,则点C的坐标是( )
- A.
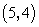
- B.
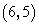
- C.
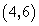
- D.
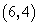
答案
正确答案:D
知识点:坐标与图形性质 正方形的性质 全等三角形的判定与性质
①如图所示,
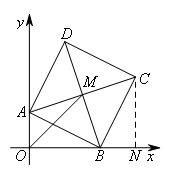
要求点C的坐标,先过点C作x轴的垂线,垂足为N.
∵AB=BC,∠ABO =90°-∠CBN=∠BCN,
∴Rt△ABO≌Rt△BCN,
∴BN=AO=2,CN=OB,
此时要求点C的坐标,我们只要求出OB的长即可.
②考虑∠AMB在坐标系中是斜直角,过点M分别作x轴、y轴的垂线,垂足分别为点E,F,如图所示:
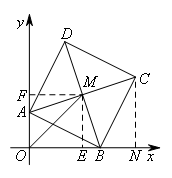
容易证明Rt△MFA≌Rt△MEB,
∴MF=ME,AF=EB,
∴矩形FOEM是正方形.
∵OM=![]() ,
,
∴OE=OF=3,
∴EB=AF=1,
∴OB=4,
则点C的坐标为(6,4).
略








