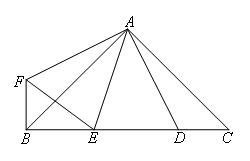
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D,E为BC边上的两点,且∠DAE=45°.连接EF,
BF,则下列结论:①△AED≌△AEF;②△ABE∽△ACD;③BE+DC>DE;④BE²+DC²=DE².
其中正确的有(    )个.

①∵∠DAE=∠FAE=45°，AD=AF，AE=AE，
∴△AED≌△AEF，
∴原结论正确；
②∵∠ABE=∠C=45°，∠BAE+∠CAD=45°，
显然证明△ABE∽△ACD缺少一组对应角相等，
∴原结论错误；
③∵∠FAB+∠BAE=45°，∠BAE+∠DAC=45°，
∴∠FAB=∠DAC
∵AB=AC，AF=AD，
∴△FAB≌△DAC，
∴BF=DC，
∵BE+BF＞EF，
由①全等可知，EF=DE，
∴BE+DC＞DE，
∴原结论正确；
④由③中全等可知，∠FBA=∠C=45°，
∴∠FBE=90°，
则在Rt△FBE中，BE²+BF²=EF²，
∵BF=DC，
∴BE²+DC²=EF²，
由①中全等可知，EF=DE，
∴BE²+DC²=DE²，
∴原结论正确

略