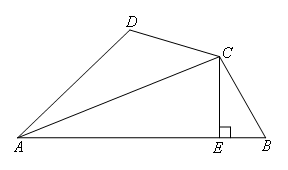
如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,并且AE=,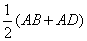
那么∠ABC+∠ADC的度数为(    )

（1）考点：全等三角形的性质与判定
（2）解题过程：
解：如图，过点C作CF垂直于AD，交AD的延长线于点F

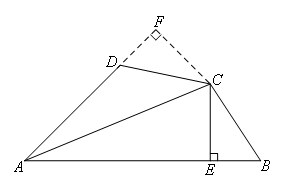
∵AC平分∠BAD
∴∠FAC=∠EAC
∵CE⊥AB，CF⊥AD
∴∠AFC=∠AEC=90°
∵AC=AC
∴△AFC≌△AEC(AAS)
∴AF=AE，CF=CE
∵AE＝(AB＋AD)
∴2AE=AB+AD
∵AD=AF-DF，AB=AE+BE，AF=AE
∴2AE=AE+BE+AE-DF，
∴BE=DF，
∵∠DFC=∠CEB=90°，CF=CE
∴△CDF≌△CEB
∴∠ABC=∠CDF
∵∠ADC+∠CDF=180°
∴∠ABC+∠ADC=180°
故选A

略