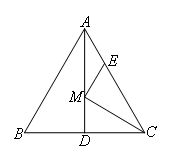
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,
若AE=2,EM+CM的最小值为( )
- A.4
- B.8
- C.
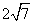
- D.
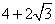
答案
正确答案:C
知识点:轴对称-最短路线问题
如图,
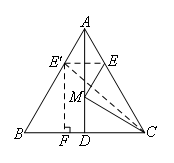
∵等边三角形为轴对称图形,对称轴为三线合一那条线段所在直线
∴点E关于直线AD的对称点E′必在线段AB上,AE′=AE=2
连接CE′,则CE′的长即为所求.
过点E′作E′F⊥BC,垂足为F
∵AE′=2,AB=6
∴BE′=4
在Rt△BE′F中,∠B=60°
∴BF=2,![]()
∴CF=4
在Rt△CE′F中,由勾股定理,得
![]()
故选C
略








