如图,在直角梯形ABCD中,∠D=∠C=90°,AD∥BC,∠DAB的平分线交CD于点E,且BE恰好平分∠ABC,则下列结论中错误的是( )
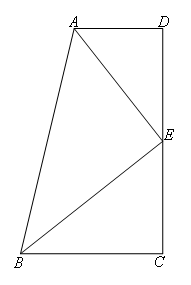
- A.AE⊥BE
- B.CE=DE
- C.AD+DE=BE
- D.AB=AD+BC
答案
正确答案:C
知识点:三角形全等之截长补短
解:如图,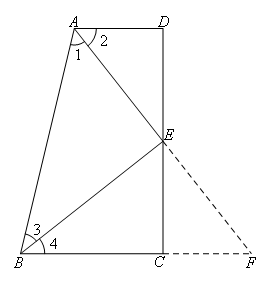
选项A:
∵AD∥BC
∴∠DAB+∠ABC=180°
∵AE平分∠DAB,BE平分∠ABC
∴∠1=∠2,∠3=∠4
即∠1+∠2+∠3+∠4=180°
∴∠1+∠3=90°
∴∠AEB=90°,则AE⊥BE.故A正确.
选项B: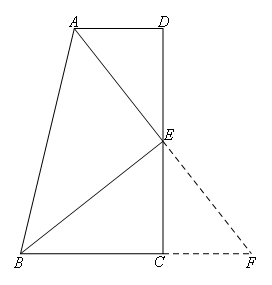
延长AE交BC的延长线于点F.
∵AD∥BC,AE是∠DAB的角平分线,
∴∠DAF=∠BAE=∠AFB,
∴AB=BF,
∴△ABF是等腰三角形;
又由①知AE⊥BE,
∴AE=FE,
在△FEC和△AED中,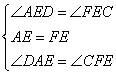
∴△FEC≌△AED(ASA),
∴DE=CE
故B正确
选项C:不正确
选项D:由△FEC≌△AED可知,
AD=CF
∴BF=BC+AD
∴AB=AD+BC
故D正确
略








