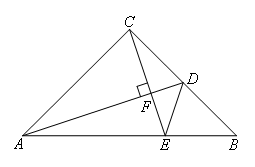
如图所示,△ABC是等腰直角三角形,即AC=BC,∠BAC=∠B=45°,∠ACB=90°.AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,则∠ADC与∠BDE的大小关系是( )
- A.∠ADC>∠BDE
- B.∠ADC=∠BDE
- C.∠ADC<∠BDE
- D.无法确定
答案
正确答案:B
知识点:全等三角形的判定与性质
1.思路点拨
①观察图形,结合选项猜测结果应该是∠ADC=∠BDE,接下来需要小心求证;
②要证明两个角相等,需要证明这两个角所在的三角形全等,故需寻找或构造全等三角形来解题;
③结合题目发现没有现成的全等三角形,故需构造;在构造的同时,要注意题目的大背景是等腰直角三角形,故可尝试作角平分线来解决问题.
2.解题过程
解:如图,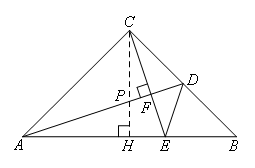
作CH⊥AB,垂足为H,CH交AD于点P,
∵在Rt△ABC中,AC=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°
∴∠HCA=90°-∠HAC=45°=∠BCH
∵∠CAP+∠CDA=90°,∠DCE+∠ADC=90°
∴∠CAP=∠BCE
在△ACP和△CBE中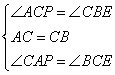
∴△ACP≌△CBE(ASA)
∴CP=BE
在△DCP和△DBE中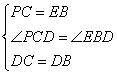
∴△DCP≌△DBE(SAS)
∴∠CDP=∠BDE
即∠ADC=∠BDE,
故选B
3.易错点
①缺乏有理有据的推导,遇到难题缺乏有序探索,直接猜测答案后不去验证;
②对于如何证明两个三角形全等,不知道借助题目的大背景来作辅助线.
略








