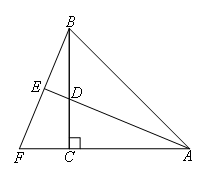
如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BF⊥AD,AD的延长线交BF于E,且E为垂足,则有以下结论①AD=BF;②CF=CD;③AC+CD=AB;④BE=CF;⑤BF=2BE.其中正确的结论有(    )个.

∵BC=AC，∠ACB=90°，
∴∠CAB=∠ABC=45°，
∵AD平分∠BAC，
∴∠BAE=∠EAF=22.5°，
∴Rt△ADC≌Rt△BFC（ASA），
∴AD=BF，CF=CD
故①②正确；

∵Rt△ADC≌Rt△BFC，
∴CF=CD，AC+CD=AC+CF=AF，
∵∠CBF=∠EAF=22.5°，
∴在Rt△AEF中，∠F=90°-∠EAF=67.5°，
∵∠CAB=45°，
∴∠ABF=180°-∠F-∠CAB=180°-67.5°-45°=67.5°，
∴AF=AB，即AC+CD=AB，
故③正确；

∵△ABF是等腰三角形，
∵BE⊥AD，
∴，
∵在Rt△BCF中，若BE=CF，则∠CBF=30°，与∠CBF=22.5°相矛盾，
故BE≠CF，
故④错误；

∵△ABF是等腰三角形，
∵BE⊥AD，
∴BF=2BE，
故⑤正确．
所以①②③⑤四项正确．
故选A．

略