在△ABC中,∠BCA=90°,AC=BC,分别过点A,点B向经过C的直线CD作垂线,垂足分别为E,F,若AE=5,BF=3,则EF的值为(    )

1.思路点拨：这是一道几何题，但是并没有图形，所以需要我们警惕是否需要分类讨论，根据题目中的描述，可知CD的位置有两种情况，如图所示，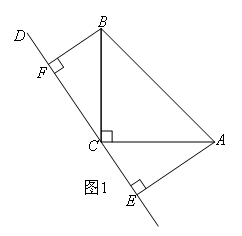

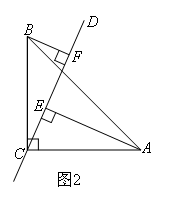
2.解题过程：
①如图1，
∵∠BCA=90°
∴∠BCF+∠ACE=90°
又∵AE⊥CD，BF⊥CD
∴∠ACE+∠CAE=90°
∴∠BCF=∠CAE
在△BCF和△CAE中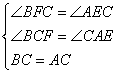

∴△BCF≌△CAE（AAS）
∴CF=AE=5，CE=BF=3
∴EF=CF+CE=5+3=8．
②如图2，
同理可证明△BCF≌△CAE（AAS），得到CF=AE=5，CE=BF=3
∴EF=CF-CE=5-3=2．
综上，EF=2或8
故选D
3.易错点：
①没有进行分类讨论；
②未能根据题意画出符合题意的图形，妄自猜测得到答案.

略