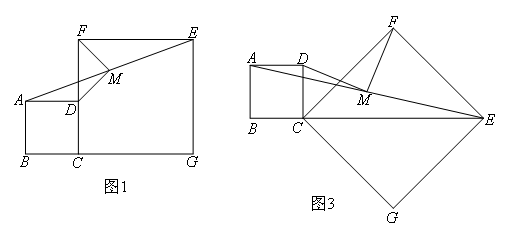
如图1,在正方形ABCD和正方形CGEF(CG>BC)中,点B,C,G在同一直线上,点M是AE的中点.
(3)将图1中的正方形CGEF绕点C顺时针旋转,使正方形CGEF的对角线CE恰好与正方形ABCD的边BC在同一条直线上,如图3,其他条件不变,则MD与MF的数量及位置关系是(    )

1．思路点拨：
①观察图形，对比前两题和本题的图形和问法，可以判断，这是一道类比探究题，而解决类比探究题，核心在于照搬，照搬字母，照搬辅助线，照搬结论.
②本题中考虑照搬思路，继续利用倍长中线来证明全等，利用全等来转移条件，故仍然延长DM交CE于点N，证明△DFN为等腰直角三角形.
2．解题过程：
如图，

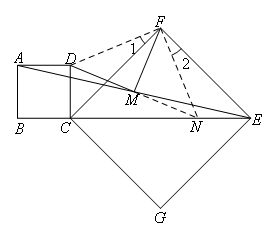
延长DM交CE于点N，连接DF，FN．
∵AD∥BE
∴∠DAM=∠NEM
在△AMD与△EMN中，

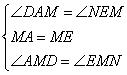
∴△AMD≌△EMN(ASA)
∴AD=EN，MD=MN
∵AD=CD
∴EN=CD
在等腰直角△CFE中，∠FCE=∠FEC=45°
∴∠DCF=45°
在△DCF和△NEF中

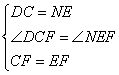
∴△DCF≌△NEF（SAS）
∴DF=NF，∠1=∠2
∵∠2+∠CFN=90°
∴∠1+∠CFN =90°
即∠DFN=90°
在△DMF和△NMF中

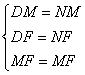
∴△DMF≌△NMF（SSS）
∴∠DMF=∠EMF=90°，∠DFM=∠EFM=45°
∵∠MDF=45°
∴△MDF也为等腰直角三角形
即MD=MF，MD⊥MF
故选D
3．易错点：
①不能结合图形，条件和问法辨识类比探究的类型，把题目割裂开来做；
②对于类比探究照搬思想理解不到位，不知道照搬什么，如何照搬；
视频推荐：“2013~2014八年级上册数学拔高课人教版——第1课初中数学全等三角形拔高课——第5讲类比探究”.

略