1编号:139593题型:解答题测试正确率:0%
如图,在Rt△ABC中,∠ACB=90°,∠BAC=α,点D在边AC上(不与点A,C重合),连接BD,点K为线段BD的中点,过点D作DE⊥AB于点E,连接CK,EK,CE,将△ADE绕点A顺时针旋转一定的角度(旋转角小于90°).
(1)如图1,若α=45°,则△ECK的形状为 ;
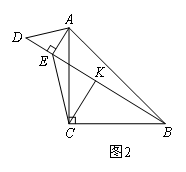
(2)在(1)的条件下,若将图1中的△ADE绕点A旋转,使得D,E,B三点共线,点K为线段BD的中点,如图2所示,求证:BE-AE=2CK;
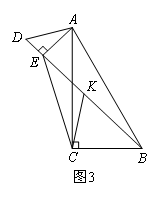
(3)若△ADE绕点A旋转至图3位置时,使得D,E,B三点共线,点K仍为线段BD的中点,请你直接写出BE,AE,CK三者之间的数量关系(用含α的三角函数表示).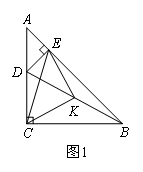
2编号:139524题型:解答题测试正确率:0%
3编号:139357题型:解答题测试正确率:0%
数学课上,张老师出示了如下题目.
如图,在△ABC中,∠A=90°,AB=AC,点D为BC的中点,点E和点F分别是边AB和AC上的点,且始终满足DE⊥DF,试确定DE与DF的大小关系.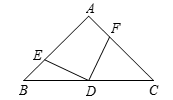
小明与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
如图1,若点E与点A重合时,点F与点C重合,容易得到DE与DF的大小关系.请你直接写出结论:DE DF(填“>”,“<”或“=”).
(2)特例启发,解答题目
如图2,若点E不与点A重合时,DE与DF的大小关系是:DE DF(填“>”,“<”或“=”).理由如下:连接AD.(请你完成剩下的解答过程)
(3)拓展结论,设计新题
在△ABC中,∠A=90°,AB=AC,点D为BC的中点,点E和点F分别是直线AB和直线AC上的点,且始终满足DE⊥DF,若AB=AC=1,BE=2,求CF的长.(请你直接写出结果)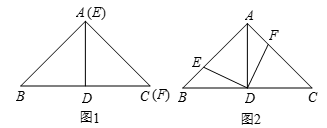
4编号:139205题型:解答题测试正确率:0%
(2021武汉)问题提出
如图1,在△ABC和△DEC中,∠ACB=∠DCE=90°,BC=AC,EC=DC,点E在△ABC内部,直线AD与BE交于点F.线段AF,BF,CF之间存在怎样的数量关系?
问题探究
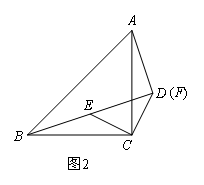
(1)先将问题特殊化如图2,当点D,F重合时,直接写出一个等式,表示AF,BF,CF之间的数量关系;
(2)再探究一般情形如图1,当点D,F不重合时,证明1中的结论仍然成立.
问题拓展
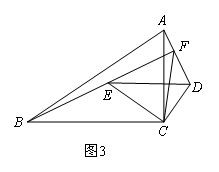
如图3,在△ABC和△DEC中,∠ACB=∠DCE=90°,BC=kAC,EC=kDC(k是常数),点E在△ABC内部,直线AD与BE交于点F.直接写出一个等式,表示线段AF,BF,CF之间的数量关系.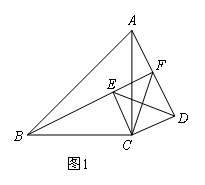
5编号:139111题型:解答题测试正确率:0%
6编号:139087题型:解答题测试正确率:0%
7编号:138720题型:解答题测试正确率:0%
8编号:137426题型:解答题测试正确率:0%
9编号:137380题型:解答题测试正确率:0%
(2021赤峰)数学课上,有这样一道探究题.
如图,已知△ABC中,AB=AC=m,BC=n,∠BAC=α(0°<α<180°),点P为平面内不与点A,C重合的任意一点,连接CP,将线段CP绕点P顺时针旋转α,得线段PD,连接CD,AP,点E,F分别为BC,CD的中点,设直线AP与直线EF相交所成的较小角为β,探究![]() 的值和β的度数与m,n,α的关系.
的值和β的度数与m,n,α的关系.
请你参与学习小组的探究过程,并完成以下任务:
(1)填空:
问题发现
小明研究了α=60°时,如图1,求出了![]() 的值和β的度数分别为
的值和β的度数分别为![]() = ,β= ;
= ,β= ;
小红研究了α=90°时,如图2,求出了![]() 的值和β的度数分别为
的值和β的度数分别为![]() = ,β= ;
= ,β= ;
类比探究
他们又共同研究了α=120°时,如图3,也求出了![]() 的值和β的度数;
的值和β的度数;
归纳总结
最后他们终于共同探究得出规律:![]() = (用含m,n的式子表示);β= (用含α的式子表示).
= (用含m,n的式子表示);β= (用含α的式子表示).
(2)求出α=120°时![]() 的值和β的度数.
的值和β的度数.


10编号:136996题型:解答题测试正确率:0%
(1)操作发现
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①请按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的对应点为点B′,点C的对应点为点C′,
连接BB′;
②在①中所画图形中,∠AB′B= °.
(2)问题解决
如图2,在Rt△ABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到
AE,连接DE,求∠ADE的度数.
(3)拓展延伸
如图3,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k为常数),求BD的长(用含k的式子表示).

