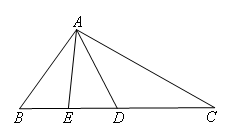
已知:如图,在△ABC中,D为BC边中点,∠BDA=∠BAD,E为BD中点,连接AE.则下列结论不正确的是(    )

1．思路点拨
①判断类型，这是一个多结论问题，需要我们对题目中的结论进行一一分析
②具体操作，根据题目中的条件易说明BC=2AB，
∴A选项正确，但是B，C，D这三个结论都不易证明.
所以需要我们再重新审视题干中的条件，发现有中点，这个条件很重要，我们知道见中点（中线）要倍长，倍长之后证全等，利用全等转移条件，但是D和E均为中点，倍长AD还是
AE呢？结合C选项AC=2AE，可知倍长AE，然后证明全等转移条件就可得到正确结论.
2．解题过程
如图，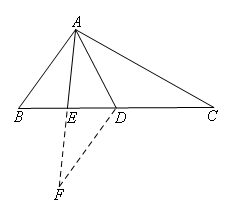

延长AE到F，使得EF=AE，连接DF.
∵E为BD中点
∴BE=ED
在△ABE和△FDE中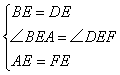

∴△ABE≌△FDE（SAS）
∴AB=FD，∠BAF=∠F，∠B=∠FDE
∵∠BDA=∠BAD
∴BD=AB
∵D为BC边中点
∴CD=BD=AB=FD
∵∠BDA=∠BAD
∴∠ADF=∠BDA+∠FDE，∠ADC=∠B+∠BAD
即∠ADF=∠ADC
在△FAD和△CAD中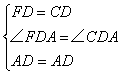

∴△FAD≌△CAD（SAS）
∴∠F=∠C，AC=AF=2AE
∴∠C=∠BAE
∴C，D正确
而B选项AB和AD不一定相等.
故选B

略