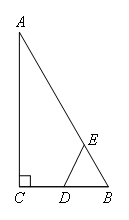
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
- A.2
- B.2.5或3.5
- C.3.5或4.5
- D.2或3.5或4.5
答案
正确答案：D
△BDE是直角三角形时，△BDE相似于△ACB，三边关系之比为
，
已知AB=2BC=4，
，
若∠DEB=90°，
当A→B时，
，
∴t=3.5；
当B→A，t=4+0.5=4.5．
若∠EDB=90°，
当A→B时，BE=2BD=2，
∴t=2；
当B→A，t=4+2=6（舍去）．
综上可得，t的值为2或3.5或4.5．
略
WORD格式（
