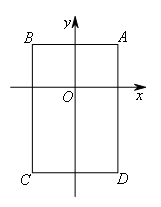
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A……的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(    )

由A，B，C，D四点的坐标可知，四边形ABCD为长方形
∵A（1，1），B（-1，1），C（-1，-2），D（1，-2），
∴AB=1-（-1）=2，BC=1-（-2）=3，CD=1-（-1）=2，DA=1-（-2）=3，
∴绕长方形ABCD一周所用的细线长度为2+3+2+3=10
∵2012=20110+2，
∴细线围着长方形ABCD绕了201圈后剩余2个单位长度
∵AB=2，
∴细线另一端在B点，坐标为（-1，1）
故选B

略