如图,已知∠AOB=30°,P为∠AOB内一点,OP=6cm,点P关于OA,OB的对称点分别为C,D,连接CD,交OA于M,交OB于N,连接OC,OD,则△PMN的周长为( )
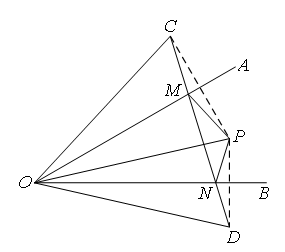
- A.3cm
- B.6cm
- C.9cm
- D.12cm
答案
正确答案:B
知识点:轴对称的性质 等边三角形的判定及性质
∵C,D分别是点P关于OA,OB的对称点,
∴∠COA=∠AOP,∠DOB=∠BOP,
PM=CM,PN=DN,CO=PO=DO,
∴∠COD=∠COA+∠AOP+∠DOB+∠BOP=2∠AOB,
∵∠AOB=30°,
∴∠COD=60°,
∴△OCD是等边三角形,
∴CD=OC=OC=OP=6
又∵PM+MN+PN=CM+MN+ND=CD,
∴PM+MN+PN=6
即△PMN的周长为6.
故选B
略








