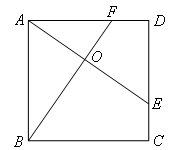
如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,有下列结论:①AE=BF;②AE⊥BF;③AO=OE;④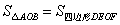.其中正确的有(    )

①∵四边形ABCD为正方形，
∴AB=AD=DC，∠BAD=∠D=90°．
∵CE=DF，
∴AF=DE，
∴△ABF≌△DAE，
∴AE=BF．故结论①正确．
②由①得，∠ABF=∠DAE．
∵∠DAE+∠EAB=90°，
∴∠ABF+∠EAB=90°，
∴∠AOB=90°，
∴AE⊥BF．故结论②正确．
③如图，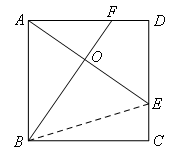

连接BE，
若AO=OE成立，则得到AB=BE，
而，
∴AO=OE不成立．故结论③错误．
④由①得，△ABF≌△DAE，
∴，
∴，
∴．故结论④正确．
故选B．

略