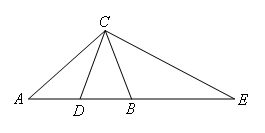
如图,CB,CD分别是钝角三角形AEC和锐角三角形ABC的中线,且AC=AB,给出下列结论:
①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB平分∠DCE.其中一定正确的结论序号为(    )

①由题意得，AE=2AB=2AC．故结论①正确．
②由题意得，
AE=2AB=2AC=4AD，
∴．
又∵∠EAC=∠CAD，
∴△EAC∽△CAD，
∴，
∴CE=2CD．故结论②正确．
③由②中△EAC∽△CAD得，∠ACD=∠E，
若∠ACD=∠BCE，则∠E=∠BCE，
可得BC=BE，
进而得到AC=AB=BC，
即△ABC为等边三角形．
而由题干条件只能说明△ABC为等腰三角形，并不能得到△ABC为等边三角形．故结论③不一定正确．
④由AC=AB得，∠ACB=∠ABC，
∴∠ACD+∠DCB=∠E+∠BCE．
∵∠ACD=∠E，
∴∠DCB=∠BCE，
∴CB平分∠DCE．故结论④正确．
故选B．

略