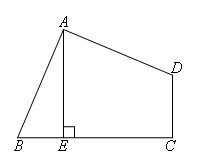
如图,在四边形ABCD中,∠BAD=∠C=90°,AE⊥BC于点E,AE=10,AB=AD.则四边形ABCD的面积为(    )

题干当中提供了一个条件AB=AD，从而在求四边形ABCD面积时，想到将△ABE绕点A旋转，使得AB与AD重合，这样构造了一个正方形，求面积比较方便，但是旋转是一种思想，具体操作如下.
如图，

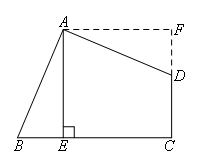
过点A作CD的垂线交CD的延长线于点F，
此时四边形AECF是矩形，
∴∠EAF=90°.
∵∠BAD=90°，
∴∠BAE=∠DAF，
∵AB=AD，∠AEB=∠F=90°，
∴△ABE≌△ADF.
∴AE=AF，且四边形ABCD的面积转化为矩形AECF的面积，
∴矩形AECF为正方形.
∵AE=10，
∴正方形AECF的面积为100，
∴四边形ABCD的面积为100.

略