如图,在△ABC中,BE,CF分别为边AC,AB上的高,D为BC的中点,DM⊥EF于点M,若BC=10,
DM=3,则EF的长为( )
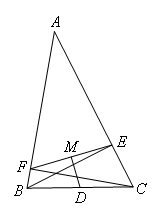
- A.6
- B.9
- C.7
- D.8
答案
正确答案:D
知识点:直角三角形斜边上的中线 勾股定理 等腰直角三角形
如图,连接DE,DF.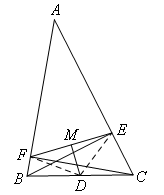
∵BE,CF分别为边AC,AB上的高,
∴∠BFC=∠BEC=90°,△BFC,△BEC为直角三角形.
∵D为BC的中点,BC=10,
∴DE=DF=5,即△DEF为等腰三角形.
又∵DM⊥EF,
∴![]() .
.
在Rt△MDF中由勾股定理得,![]() ,
,
∴![]() .
.
略








