如图,正方形ABCD的周长为24,△BCE是等边三角形,F是CE的中点,AE,BF交于点G,
连接CG,则CG的长为( )

- A.
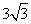
- B.
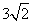
- C.
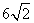
- D.
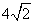
答案
正确答案:B
要求CG(=GE)的长,考虑在直角△GFC(或△GEF)中,通过勾股定理来求,FC=FE=3,此时若要求GF的长,只从边入手并不能求,所以考虑从角入手,判断能否出现特殊角或特殊的三角形,进而来求解.
由题意得,AB=BC=CD=CE=BE=6.
在等边三角形BEC中,
∵BF⊥EC,
∴EF=FC=3,即BF是CE的垂直平分线,
∴GE=GC.
∵AB=BE,∠ABE=90°+60°=150°,
∴∠BEA=15°,
∴∠GEF=45°,
即△GEF为等腰直角三角形,
∴![]() .
.
略








