在等腰三角形ABC中,∠ACB=90°,AC=1,过点C作直线l∥AB,P为直线l上一点,且AP=AB,则点P到BC所在直线的距离是( )
- A.
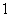
- B.
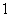 或
或
- C.
 或
或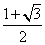
- D.
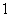 或
或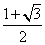
答案
正确答案:C
(1)如图1,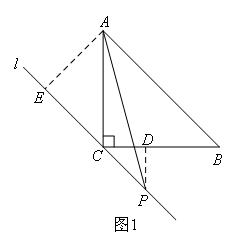
过点P作PD⊥BC于点D,过点A作AE⊥PC于点E.
∵CP∥AB,
∴∠PCD=∠ACE=∠CBA=45°.
∵在等腰直角△ABC中,AC=BC=1,AB=AP,
∴![]() ,
,![]() ,
,
∴在Rt△AEP中,![]() ,
,
∴ ,
,
解得,![]() ,
,
∴![]() .
.
在等腰直角△PCD中,可得![]() .
.
(2)如图2,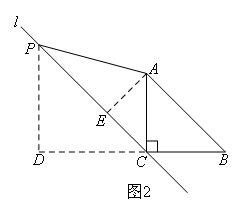
过点P作PD⊥BC交BC延长线于点D,过点A作AE⊥PC于点E.
同理可证,![]() ,
,![]() ,
,
∴在Rt△AEP中,![]() ,
,
∴ ,
,
解得,![]() ,
,
∴![]() .
.
在等腰直角△PCD中,可得![]() .
.
综上,点P到BC所在直线的距离为![]() 或
或![]() .
.
略







