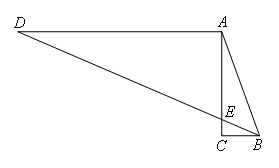
如图,AD∥BC,AC⊥BC于C,BD和AC相交于E,且DE=2AB.若∠BAC=24°,则∠DBC的度数为( )
- A.21°
- B.22°
- C.23°
- D.24°
答案
正确答案：B
知识点：直角三角形斜边中线等于斜边一半
如图，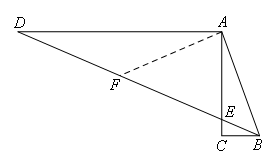
取DE的中点F，连接AF，设∠DBC=x
∵AD∥BC
∴∠DBC=∠D=x
在Rt△ADE中，DF=EF
∴
∵DE=2AB
∴AF=AB=DF
∴∠DAF=∠ADF=x，∠AFB=∠ABF=2x
∴∠BAF=90°+24°-x=114°-x
在△ABF中，
2x+2x+114°-x=180°
解得：x=22°
故选B
略
WORD格式（
