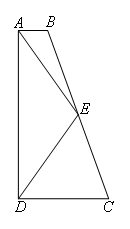
如图,在四边形ABCD中,AB∥CD,∠ADC=90°,∠C=70°,点E是BC的中点,CD=CE,则∠EAD的度数为(    )

如图，延长AE交DC的延长线于点F．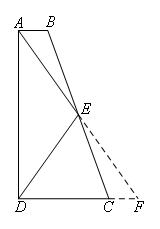

∵AB∥CD，
∴∠ABE=∠FCE，
∵点E是BC的中点，
∴BE=CE，
又∵∠AEB=∠FEC
∴△AEB≌△FEC（ASA）
∴AE=EF，
∵∠ADC=90°，
∴DE=AE=EF，
∴∠EAD=∠EDA，
∵∠C=70°，CD=CE，
∴∠CDE=55°，
∴∠EDA=35°，
∴∠EAD=35°．
故选A

略