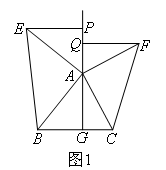
如图1,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作等腰直角三角形ABE和等腰直角三角形ACF,过点E,F作射线GA的垂线,垂足分别为点P,Q.容易证明PE=QF.
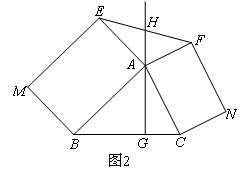
现将上面题目中向外作等腰直角三角形改为向外作矩形,如图2所示,以AB为边的矩形ABME,以AC为边的矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,则EH和HF之间的数量关系是( )
- A.
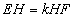
- B.
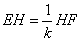
- C.
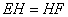
- D.
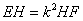
答案
正确答案:C
知识点:中考数学几何中的类比探究
分析:图1中,借助于两个弦图结构(残缺的)直接证明△EPA≌△AGB,△FQA≌△AGC,得到PE=AG=QF.这给图2中的求解提供一个思路,可以作相同的辅助线,由两个相似(图1中是全等)导出PE=QF,再判断EH和HF之间的数量关系.
如图,过点E作EP⊥GA,FQ⊥GA,垂足分别为点P,Q.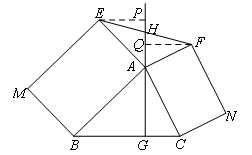
∵四边形ABME是矩形,
∴∠BAE=90°,
∴∠BAG+∠EAP=90°.
又AG⊥BC,
∴∠BAG+∠ABG=90°,
∴∠ABG=∠EAP,
∴Rt△ABG∽Rt△EAP,
∴AG:EP=AB:EA=k.
同理可证△ACG∽△FAQ,
∴AG:FQ=AC:FA=k,
∴AG:EP=AG:FQ,
∴EP=FQ.
又∵∠EHP=∠FHQ,∠EPH=∠FQH,
∴Rt△EPH≌Rt△FQH,
∴EH=HF.
略









