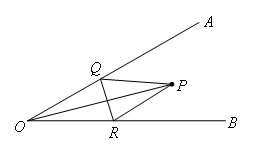
如图，∠AOB=30°，∠AOB内有一定点P，且OP=10．在OA上有一点Q，OB上有一点R．若△PQR周长最小，则最小周长是( )
- A.10
- B.15
- C.20
- D.30
答案
正确答案：A
知识点：轴对称——线段之和最小 轴对称——最值问题
点P是定点，点Q和点R是在定直线运动的动点．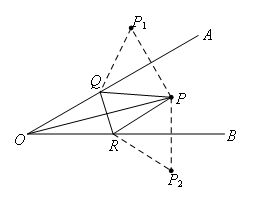
如图，分别作点P关于射线OA，OB的对称点
，连接
，使得三角形的三边转化为首尾相接的折线，此时△PQR的周长即是折线
的长，由于折线两端是定点，所以当点Q、R分别是
与OA、OB的交点时，
最小，为线段的长，如图所示．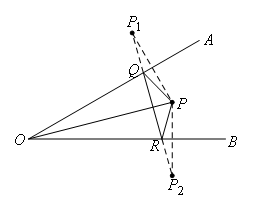
如下图，连接
，
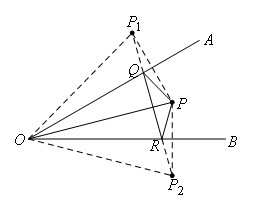
由对称可知
，
，
，
∴
，
∴
是等边三角形，
∴
即△PQR最小周长为10
略
WORD格式（
