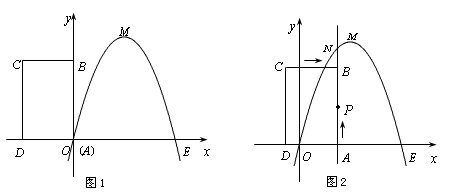（2010福建德化）如图1，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为(2,4)；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3.（1）求该抛物线的函数关系式；（2）将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）.① 当t=时，判断点P是否在直线ME上，并说明理由；②设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

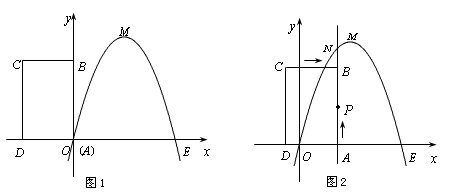
答案

（1）y=-x²+4x
（2）①点P不在直线ME上
②依题意可知：P（,），N（，）
当0<t<3时，以P、N、C、D为顶点的多边形是四边形PNDC，依题意可得：
S=S_△PCD+S_△PNC=CD·AD+=+==
∵0＜＜3
∴当=时，=.
当时,点P、N都重合，此时以P、N、C、D为顶点的多边形是三角形，依题意可得，
==3
综上所述，以P、N、C、D为顶点的多边形面积S存在最大值，最大值为

知识点：待定系数法求二次函数解析式  坐标与图形变化-平移  

（1）先计算出函数解析式；
（2）计算出t=时P点坐标，从而验证是否在ME上；
（3）画出一般情况下图形，从而选取合适的方法（分割、补形）计算面积；

一般状态下如何表达多边形的面积？

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>