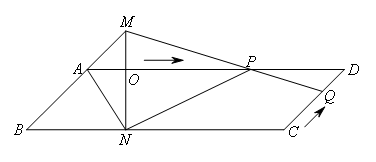
已知，如图，平行四边形ABCD中，AD=3cm，CD=1cm，∠B=45°，点P从点A出发，沿AD方向匀速运动，速度为3cm/s；点Q从点C出发，沿CD方向匀速运动，速度为1cm/s，连接QP并延长交BA的延长线于点M，过M作MN⊥BC，垂足是N，设运动时间为t（s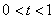）（），解答下列问题：

（1）当t=(    )时，四边形AQDM是平行四边形．

• A.
• B.
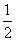
• C.
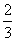
• D.

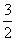
答案

正确答案：B

知识点：平行四边形的判定与性质  相似三角形的判定与性质  动点问题  

由题意，得AM∥QD，
∴∠MAP=∠QDP，∠AMP=∠DQP，
∴△AMP∽△DQP，
∴．
根据两条对角线互相平分的四边形是平行四边形可知，当AP=PD时，
四边形AQDM是平行四边形．
∵AP=3t，AD=3，
∴PD=3-3t，
∴3t=3-3t，
∴．

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>