如图,直线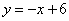 与坐标轴交于A,B两点,点P是射线AB上一点,在平面内存在一点Q,使得以O,A,P,Q为顶点的四边形是菱形,则点Q的坐标为( )
与坐标轴交于A,B两点,点P是射线AB上一点,在平面内存在一点Q,使得以O,A,P,Q为顶点的四边形是菱形,则点Q的坐标为( )
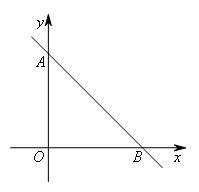
- A.
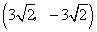 ,(-3,3)
,(-3,3) - B.(6,6),
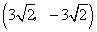 ,(-3,3)
,(-3,3) - C.(6,6),
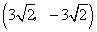 ,(-3,3),
,(-3,3),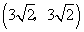
- D.(6,6),
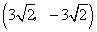 ,(-3,3),
,(-3,3),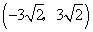
答案
正确答案:B
知识点:一次函数中的存在性问题 菱形的存在性
由题干可知,菱形的四个顶点中,点O,A为定点,点P,Q为动点,并且点P是在射线AB上运动的.
菱形是由一个等腰三角形沿着底边翻折得到的,所以菱形的存在性可以转化为等腰三角形的存在性,可以先让△OAP为等腰三角形,进而得到菱形,而要使△OAP是等腰三角形,就转化为熟悉的有两个定点的等腰三角形存在性问题.
由题意得,A(0,6),OA=6,△OAB是等腰直角三角形.
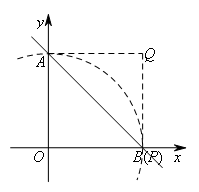
①如图,以点O为圆心,OA长为半径作圆,交射线AB于点P,易知点P和点B重合,
此时△AOP为等腰三角形,沿底边AP进行翻折,得到菱形AOPQ,
容易得到点Q的坐标为(6,6).
②如图,以点A为圆心,OA长为半径作圆,交射线AB于点P,此时△AOP为等腰三角形,沿底边OP进行翻折,得到菱形AOQP.

过点P作PD⊥OA于点D,如图所示,
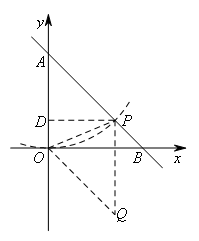
∵AP=AO=6,△ADP是等腰直角三角形,
∴![]() ,
,
∴![]() .
.
∵PQ∥AO,且PQ=AO=6,
∴![]() .
.
③如图,作AO的垂直平分线交AB于点P,此时△AOP是等腰三角形,沿底边AO进行翻折,得到菱形APOQ.
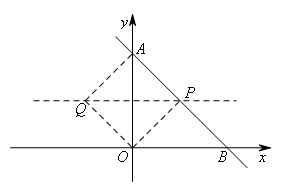
容易求得点P(3,3),点Q(-3,3).
综上,点Q的坐标为(6,6),![]() ,(-3,3).
,(-3,3).
略








