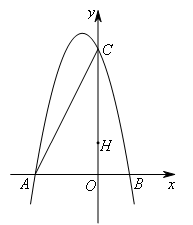
如图,抛物线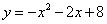 与x轴交于点A(-4,0),B(2,0),与y轴交于
与x轴交于点A(-4,0),B(2,0),与y轴交于
点C(0,8).已知点H(0,2),在y轴左侧的抛物线上存在点G,使得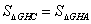 ,则点G的坐标为( )
,则点G的坐标为( )
- A.
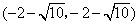 或
或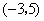
- B.
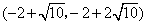 或
或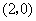
- C.
 或
或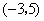
- D.
 ,
,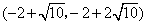 ,
,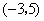 或
或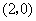
答案
正确答案:C
知识点:转化法(等底或等高)求面积 二次函数背景下的面积问题 坐标系中的面积问题
点A,C,H是定点,点G为动点,要确定使得![]() 时点G的坐标,需分类讨论:
时点G的坐标,需分类讨论:
如图,当点A,C在直线GH的同侧时,
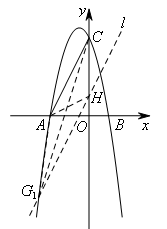
过点H作直线![]() ∥AC,与y轴左侧的抛物线交于点
∥AC,与y轴左侧的抛物线交于点![]() ,此时
,此时![]() .
.
易求得直线AC的表达式为y=2x+8,
由点H(0,2),![]() ∥AC可求得直线
∥AC可求得直线![]() 的表达式为y=2x+2,
的表达式为y=2x+2,
由![]() ,得
,得
![]() 或
或![]() (舍去),
(舍去),
∴![]() .
.
如图,当点A,C在直线GH的异侧时,
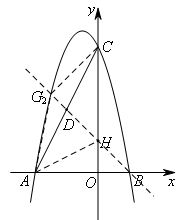
取AC的中点D,直线DH与y轴左侧的抛物线交于点![]() ,此时
,此时![]() .
.
易得D(-2,4).
设直线DH的表达式为y=kx+b,把点D,H的坐标代入得,
![]() ,
,
∴![]() ,
,
∴y=-x+2,
由![]() ,得
,得
x=-3或x=2(舍去),
∴![]() .
.
综上得,点G的坐标为![]() 或
或![]() .
.
略








