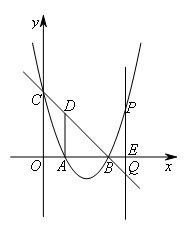
如图,抛物线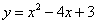 与x轴交于A,B两点,与y轴交于点C,AD⊥x轴交BC于点D,点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交直线BC于点Q,若点P的横坐标为m,当以A,D,P,Q为顶点的四边形是平行四边形时,m的值为( )
与x轴交于A,B两点,与y轴交于点C,AD⊥x轴交BC于点D,点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交直线BC于点Q,若点P的横坐标为m,当以A,D,P,Q为顶点的四边形是平行四边形时,m的值为( )
- A.
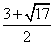
- B.2或
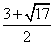 或
或 或
或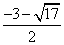
- C.2或
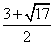 或
或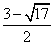
- D.2或
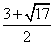
答案
正确答案:D
知识点:二次函数与几何综合 平行四边形的存在性 平行四边形的性质与判定
由题意得,点A(1,0),B(3,0),C(0,3),
∴直线BC:![]() ,
,
∴D(1,2),
∴AD=2.
以A,D,P,Q为顶点的四边形中,A,D为定点,若此四边形为平行四边形,则需按照把线段AD当作平行四边形的边或对角线来进行分类,
由题意得PQ∥AD,所以AC只能当作边来处理.
则以A,D,P,Q为顶点的四边形是平行四边形时,只需要满足PQ=AD即可.
①当![]() 时,点Q在点P的上方,如图所示,
时,点Q在点P的上方,如图所示,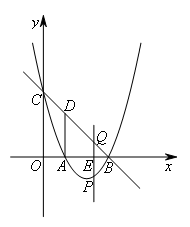
由题意得,![]() ,
,
∴![]() ,
,
当PQ=AD=2时,![]() ,
,
解得![]() ,均符合条件,但m=1时,点P和点A重合,舍去,
,均符合条件,但m=1时,点P和点A重合,舍去,
∴m的值为2.
②当![]() 时,点P在点Q的上方,如图所示,
时,点P在点Q的上方,如图所示,
∵![]() ,
,
∴![]() ,
,
当PQ=AD=2时,![]() ,
,
解得![]() ,
,
∴m的值为![]() .
.
综上所述,m的值为2或![]() .
.
略







