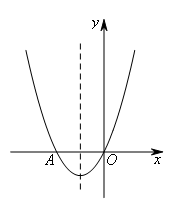
如图，已知抛物线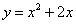经过点A（-2，0）及原点O，点B在抛物线上，点C在抛物线的对称轴上，若以点A，O，B，C为顶点的四边形是平行四边形，则点B的坐标为(    )

点A，O为定点，点B，C的位置不确定，要使以点A，O，B，C为顶点的四边形是平行四边形，需从定点A，O连成的定线段AO分析起．
由于A，O，B，C四点的位置关系不确定，
故把AO当成平行四边形的边或对角线来分类讨论．
如图，当AO为边时，BC∥AO且BC=AO=2，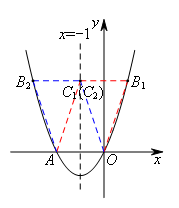

结合图象可得，，，，
∴．
如图，当AO为对角线时，

设对称轴与x轴交于点D，则点D为AO的中点，点D的坐标为（-1，0）．
点为对称轴与抛物线的交点，即抛物线的顶点，故．
综上得，点B的坐标为（1，3），（-3，3）或（-1，-1）．

略