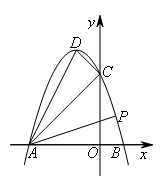
如图,抛物线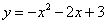 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D,连接DA,DC,AC.点P为第一象限内抛物线上一动点,若∠PAB=∠DAC,则点P的坐标为( )
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D,连接DA,DC,AC.点P为第一象限内抛物线上一动点,若∠PAB=∠DAC,则点P的坐标为( )
- A.
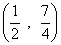
- B.
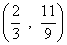
- C.
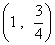
- D.
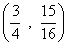
答案
正确答案:B
知识点:二次函数背景下的存在性问题
在∠PAB,∠DAC中,只有点P是动点,所以首先要研究清楚定角∠DAC具有什么性质(一般放到直角三角形中,研究三角函数值),再去和∠PAB对应.
由题意得,![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴△AOC是等腰直角三角形,![]() ,∠ACO=45°.
,∠ACO=45°.
如图,过点D作DE⊥y轴于点E,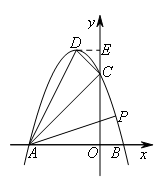
则DE=CE=1,
∴△EDC是等腰直角三角形,![]() ,∠DCE=45°,
,∠DCE=45°,
∴∠ACD=90°,![]() .
.
接下来需要把∠PAB放到直角三角形中,且这个角的正切值为![]() .
.
如图所示,过点B作BF⊥x轴交直线AP于点F,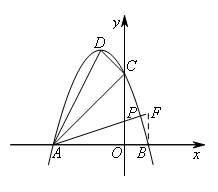
在Rt△ABF中,![]() ,
,
∵![]() ,
,
∴直线AF:![]() ,
,
联立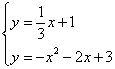 ,解得
,解得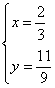 或
或![]() ,
,
∴点P的坐标为![]() .
.
略








