如图,抛物线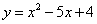 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D与点C关于抛物线的对称轴对称,连接AC,AD.P是x轴上方抛物线上一点,若∠ADP=∠ACO,则点P的坐标为( )
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D与点C关于抛物线的对称轴对称,连接AC,AD.P是x轴上方抛物线上一点,若∠ADP=∠ACO,则点P的坐标为( )
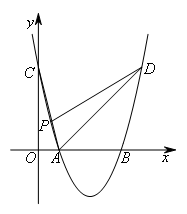
- A.
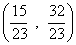
- B.

- C.
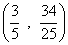
- D.
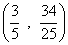 或
或
答案
正确答案:C
知识点:三等角模型 二次函数背景下的存在性问题
由题意得,A(1,0),B(4,0),C(0,4),D(5,4).
在∠ADP和∠ACO中,首先需要弄清楚定角∠ACO具有何种性质.
在Rt△OCA中,![]() .
.
接下来需要把∠ADP放到直角三角形中,且这个角的正切值为![]() .
.
如图所示,过点A作AE⊥AD交DP的延长线于点E,
过点E作EF⊥x轴于点F(此时点O和点F重合,下方有解释),
过点D作DG⊥x轴于点G,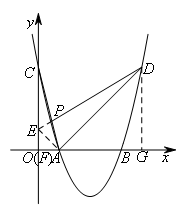
由三等角模型可知△EFA∽△AGD,且相似比为1:4,
∵D(5,4),A(1,0),
∴GA=GD=4,
∴EF=FA=1,
∴点F与点O重合,E(0,1),
∴直线DP:![]() .
.
联立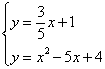 ,解得
,解得 或
或![]() ,
,
∴点P的坐标为![]() .
.
略








