如图,抛物线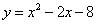 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D为顶点,抛物线的对称轴与x轴交于点E,连接BD,CD.P为对称轴右侧的抛物线上一点,若满足
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D为顶点,抛物线的对称轴与x轴交于点E,连接BD,CD.P为对称轴右侧的抛物线上一点,若满足
∠DCP=∠DBE,则点P的坐标为( )
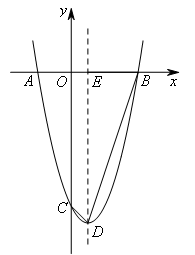
- A.
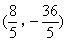
- B.
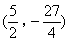
- C.(4,-6)
- D.
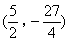 或(0,-8)
或(0,-8)
答案
正确答案:B
知识点:三等角模型 二次函数背景下的存在性问题
由题意,得A(-2,0),B(4,0),C(0,-8),D(1,-9),E(1,0),
∴BE=3,DE=9.
在Rt△DEB中,![]() .
.
如图,过点D作CD的垂线,交CP的延长线于点F,
过点D作DG⊥y轴于点G,
过点F作y轴的平行线,交GD的延长线于点H,此时FH⊥DH.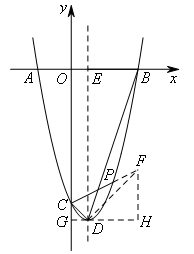
在Rt△CDF中,![]() .
.
易求得,CG=GD=1.
由△CGD∽△DHF得,![]() ,
,
∴DH=HF=3,
∴点F的坐标为(4,-6).
由C,F两点的坐标得直线CF的表达式为![]() .
.
由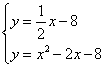 得,
得, ,
,
∴点P的坐标为![]() .
.
略








