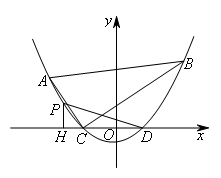
如图,已知二次函数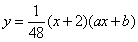 的图象经过A(-4,3),B(4,4)两点,与x轴交于C,D两点(点C在点D的左侧).P为第二象限内的抛物线上一动点,过点P作PH⊥x轴于点H,
的图象经过A(-4,3),B(4,4)两点,与x轴交于C,D两点(点C在点D的左侧).P为第二象限内的抛物线上一动点,过点P作PH⊥x轴于点H,
若△PHD与△ABC相似,则点P的坐标为( )
- A.
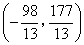
- B.
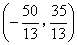 或
或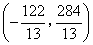
- C.
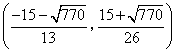 或
或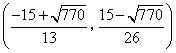
- D.
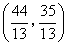 或
或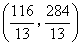
答案
正确答案:B
首先需要求出二次函数的解析式,然后再对所求目标进行研究.
将A,B两点的坐标代入表达式得,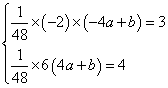 ,
,
解得![]() ,
,
∴二次函数的表达式为![]() ,
,
∴C(-2,0),![]() .
.
在△PHD与△ABC中,△ABC是由定点构成的三角形,首先研究△ABC具有何种性质.
根据勾股定理易求,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴△ABC是直角三角形,且两直角边之比为1:2.
△PHD是动的直角三角形,若△PHD和△ABC相似,则需要![]() 或
或![]() ,
,
设点P的横坐标为t(![]() ),则
),则![]() ,
,
∴![]() ,
,![]() .
.
①当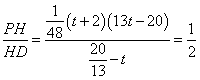 时,
时,
解得![]() ,此时点P的坐标为
,此时点P的坐标为![]() .
.
②当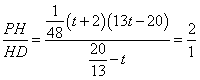 时,
时,
解得![]() ,此时P点的坐标为
,此时P点的坐标为![]() .
.
综上所述,P点的坐标为![]() 或
或![]() .
.
略








