已知抛物线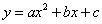 经过A(-3,0),B(0,3),C(1,0)三点.
经过A(-3,0),B(0,3),C(1,0)三点.
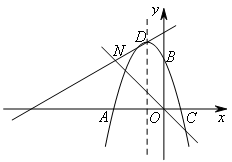
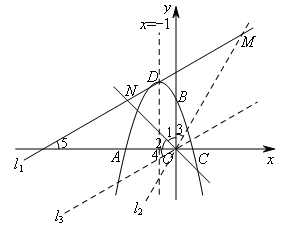
(1)如图,将抛物线的对称轴绕抛物线的顶点D顺时针旋转60°,与直线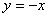 交于点N.若在直线DN上存在一点M,使得∠MON=75°,则点M的坐标为( )
交于点N.若在直线DN上存在一点M,使得∠MON=75°,则点M的坐标为( )
- A.

- B.
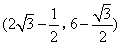
- C.
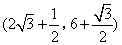
- D.
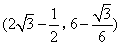
答案
正确答案:C
知识点:二次函数与几何综合
设抛物线的表达式为![]() ,
,
把点C坐标(1,0)代入得,a=-1,
∴抛物线的表达式为![]() ,对称轴为直线x=-1,顶点为D(-1,4).
,对称轴为直线x=-1,顶点为D(-1,4).
如图,由直线ON的表达式为y=-x得,∠1=∠2=45°.
易求得对称轴绕点D顺时针旋转60°之后得到的直线![]() 的表达式为
的表达式为![]() .
.
要在直线DN上找到点M,使得∠MON=75°,
需将直线ON绕点O旋转75°,再算出与直线![]() 的交点坐标即可.
的交点坐标即可.
分两种情况讨论:
如图,将直线ON绕点O顺时针旋转75°得到直线![]() ,
,![]() 与
与![]() 的交点即为要求的点M.
的交点即为要求的点M.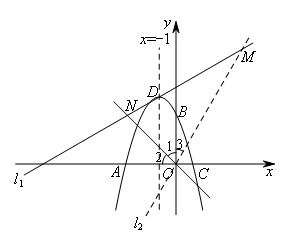
易得∠3=75°-45°=30°,直线![]() 的表达式为
的表达式为![]() .
.
由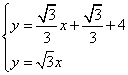 得,
得,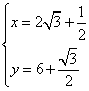 ,即点M的坐标为
,即点M的坐标为![]() .
.
如图,将直线ON绕点O逆时针旋转75°得到直线![]() .
.
易得∠4=∠5=30°,![]() ∥
∥![]() ,
,![]() 与
与![]() 没有交点,此时点M不存在.
没有交点,此时点M不存在.
综上得,点M的坐标为![]() .
.
略








