如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线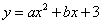 经过A,B两点,与x轴交于另一点C.若点D的坐标为(-1,0),在直线y=-x+3上存在点P,使△ABO与△ADP相似,则点P的坐标为( )
经过A,B两点,与x轴交于另一点C.若点D的坐标为(-1,0),在直线y=-x+3上存在点P,使△ABO与△ADP相似,则点P的坐标为( )
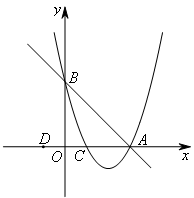
- A.(-1,4)或
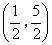
- B.(-1,3)或(1,2)
- C.(-1,4)或(1,2)
- D.(-1,4),(1,2)或(5,-2)
答案
正确答案:C
由题意得,A(3,0),B(0,3),AO=BO=3.
把A(3,0),B(0,3)代入抛物线表达式可得,![]() ,
,
∴C(1,0).
在△ABO中,点A,B,O为定点,且△ABO为等腰直角三角形.
在△ADP中,A,D为定点,点P为直线AB上的动点,
要使△ADP与△ABO相似,需△ADP为等腰直角三角形.
从直角顶点入手进行分类讨论.
当点A是直角顶点时,此时在直线y=-x+3上不存在点P使得△ADP为等腰直角三角形.
如图,当点D为直角顶点时,过点D作![]() ⊥DA,交直线AB于点
⊥DA,交直线AB于点![]() .
.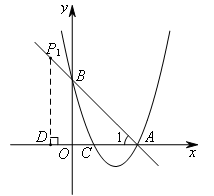
由∠1=45°可得,![]() 为等腰直角三角形,点
为等腰直角三角形,点![]() 满足题意.
满足题意.
此时![]() ,点
,点![]() 的坐标为(-1,4).
的坐标为(-1,4).
如图,当点P为直角顶点时,过点D作![]() ⊥AB于点
⊥AB于点![]() .
.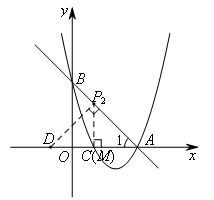
![]() 为等腰直角三角形,点
为等腰直角三角形,点![]() 满足题意.
满足题意.
过点![]() 作
作![]() 轴于点M.
轴于点M.
易得![]() ,OC=1,
,OC=1,
∴点![]() 的坐标为(1,2).
的坐标为(1,2).
综上得,点P的坐标为(-1,4)或(1,2).
略








